A Monoid Is a Category With Just One Object. So What's the Problem?

I've finally started studying Category Theory, and first step was to rename the directory with materials from the name "Cathegory" (I created it a long time ago). The book I've chosen from an excellent Quora answer by E. Kmett was "Category Theory" by Steve Awodey.

Chapter 1 hits you with a Category definition, and then a bunch of examples of a Category, one of which caught my attention. First, the Category definition:

Now, an interesting example:

A monoid (sometimes called a semi-group with unit) is a set M equipped with a binary operation · : M × M → M and a distinguished “unit” element u ∈ M such that for all x, y, z ∈ M,

$$x · (y · z) = (x · y) · z$$

and

$$u · x = x = x · u$$

Equivalently, a monoid is a category with just one object. The arrows of the category are the elements of the monoid. In particular, the identity arrow is the unit element u. Composition of arrows is the binary operation m · n of the monoid.

As a person coming mostly from the world of Types, I was somewhat confused. Many questions at once:

• "Just one object". Which object? What's its type? Any arbitrary object, no connection with arrows?
• Arrows, they're..not functions. Wouldn't you encode arrows as functions from object to object in Type Theory?
• Category definition says "for each arrow f there is a domain dom(f)". What's a domain of an arrow if that arrow isn't a function then?

Seems bizarre!

So I decided to (try to) encode it. But before that, I needed to come up with the initial picture in my head, which looked something like this:

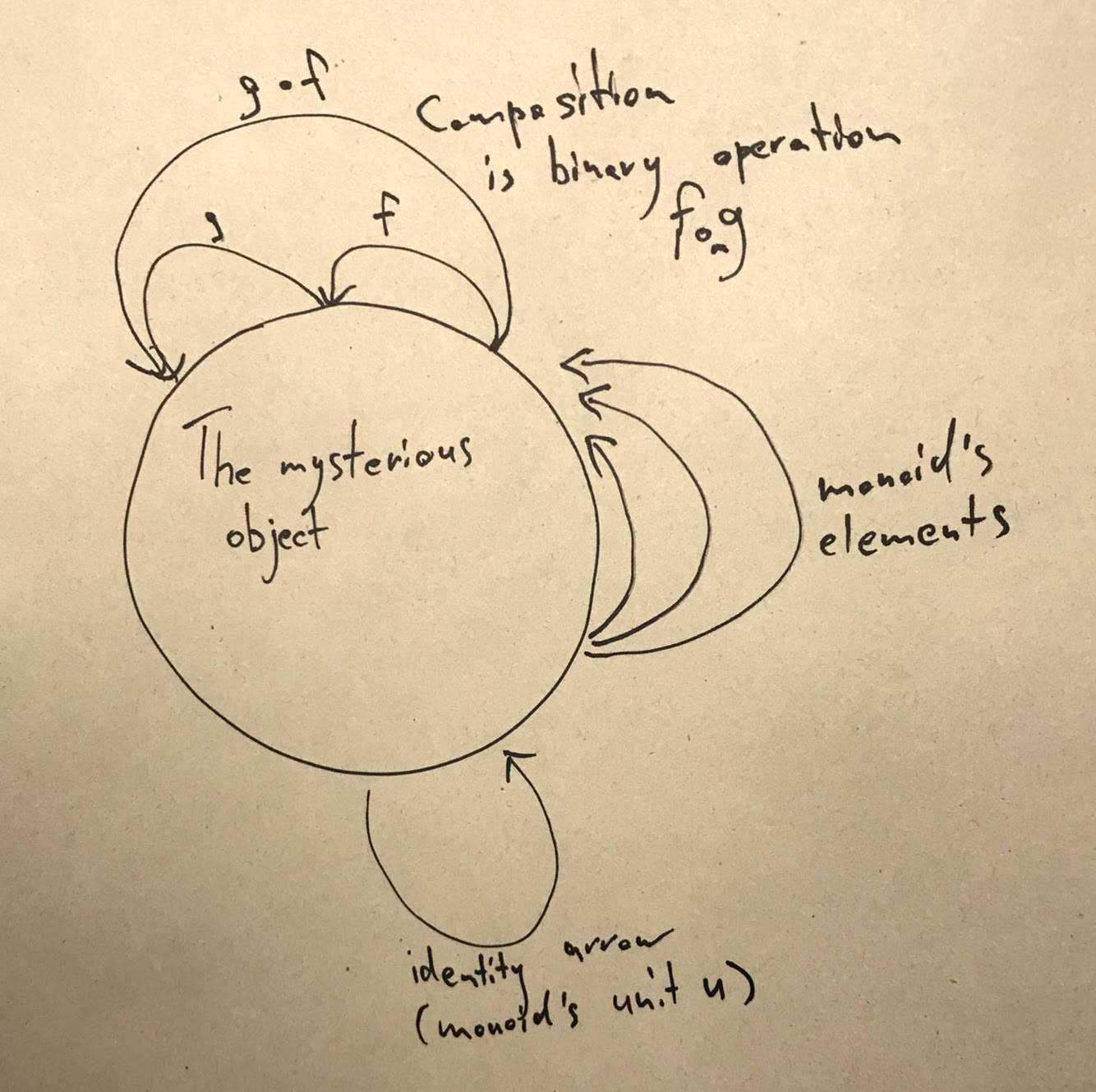
Failed attempt in CubicalTT

Initially, I started with CubicalTT because that's what I was familiar with from before and which I adore for its minimalism. Unfortunately, minimalism comes at the price of being too bare-bones. I still find it to be an excellent source for studying HoTT/MLTT, mainly because it has so much implemented in its examples directory, that I've decided to quote its definitions and my failed attempt here. If you don't understand this and want to see Agda -- don't worry! Just skip along.

​x
-- * monoid part
​
-- A Monoid is a Type that must be a SET and its laws
monoid : U
  = (X : SET) * ismonoid X
-- Monoid laws
ismonoid (M : SET) : U
  = (op : M.1 -> M.1 -> M.1)
  * (_ : isAssociative M.1 op)
  * (id : M.1)
  * (hasIdentity M.1 op id)
-- Reminder on what a SET is in HoTT
-- See lectures by Andrej Bauer for more info https://vimeo.com/330992581
-- collection of all sets (type together with laws)
SET : U = (X:U) * set X
-- for all a and b, their paths are equal (their paths are propositions)
set (A : U) : U = (a b : A) -> prop (Path A a b)
-- level of logic (type with at most
-- one element, for any two elements they are equal)
-- again, see Andrej's lecture series
prop (A : U) : U = (a b : A) -> Path A a b

and the category part:

xxxxxxxxxx
-- * category part
-- category is precategory and category laws
category : U = (C:precategory)*isCategory C
-- precategory is categoryData and precategory laws
precategory : U = (C : categoryData) * isPrecategory C
-- category data is object type and a morphism
categoryData : U = (A : U) * (A -> A -> U)

I won't quote laws here, but you can see an interesting part here already. Morphisms are represented as a type A -> A -> U, e.g. given two objects, it will provide you with a space of their morphisms. So, that space of all morphisms should be a type of the elements of our monoid's set. And a type for the object? It should always be the same, no matter what is really:

xxxxxxxxxx
data BoringMonoid = MkBoringMonoid
​
monoidToCategoryEx01 (m : monoid) : category
  = ( ( ( BoringMonoid
        , \(bm1:BoringMonoid) -> \(bm2:BoringMonoid) -> m.1.1
        )
      , ( \(x : BoringMonoid) -> m.2.2.2.1 -- monoid.ismonoid.id
        , ? -- c : (x y z : A) -> hom x y -> hom y z -> hom x z
        , ( ? -- homSet
          , ? -- cPathL
          , ? -- cPathR
          , ? -- 
          )
        )
      )
    , ? -- -- (A : cA C) -> isContr ((B : cA C) * iso C A B)
    )
​

Here, you can see something that compiles, with lots of holes for proofs of laws. Implementing proofs of laws in cubicaltt is left as an exercise for the reader!

Encoding in Agda

Hoping for a bit more user-friendliness and proof assistance, I went with Agda. It's my first experience somewhat seriously working with it, so I had to learn a lot simultaneously, including the editor setup.

First thing I've noticed in Agda, it has its library just laying around on your file system, as you set its path in ~/.agda/libraries. Which means that sources are just there to be opened. I've found Monoid in agda-stdlib/src/Algebra.agda, but couldn't find a Category.

It turned out there is no Category in agda-stdlib. Googling a bit had brought me to copumpkin/categories, but just a little later I've accidentally found the agda/agda-categories repo created 12 days ago!

A Category is a record, so the first thing to do was to make a record with holes instead of field values.Levels were done mostly by "try until it works" approach, since I haven't worked with them before, but could imagine them being somewhat trivial for our case. Loading in Emacs via C-c C-l fills holes with special labels. Interesting!

Now I've filled the "more obvious" parts with success:

xxxxxxxxxx
  record
    { Obj = BoringMonoid o
    ; _⇒_ = λ bm1 bm2 → Monoid.Carrier m
    ; _≈_ = Monoid._≈_ m
    ; id = Monoid.ε m
    ; _∘_ = Monoid._∙_ m}
​

but left with unfilled laws. And that's where Agda's magic is so useful. On the next video, you can see how I've:

• focused on a hole
• looked at its local bindings C-c C-,
• auto-populated the lambda skeleton with C-c C-r
• looked at all new local bindings again
• inserted an additional variable in scope which was my initial guess
• played with its parameters until hole fits (check via C-c C-.)
• inserted the solution C-c SPC and then refined manually

I've finished the rest in a similar fashion. Final code can be seen at solution.agda

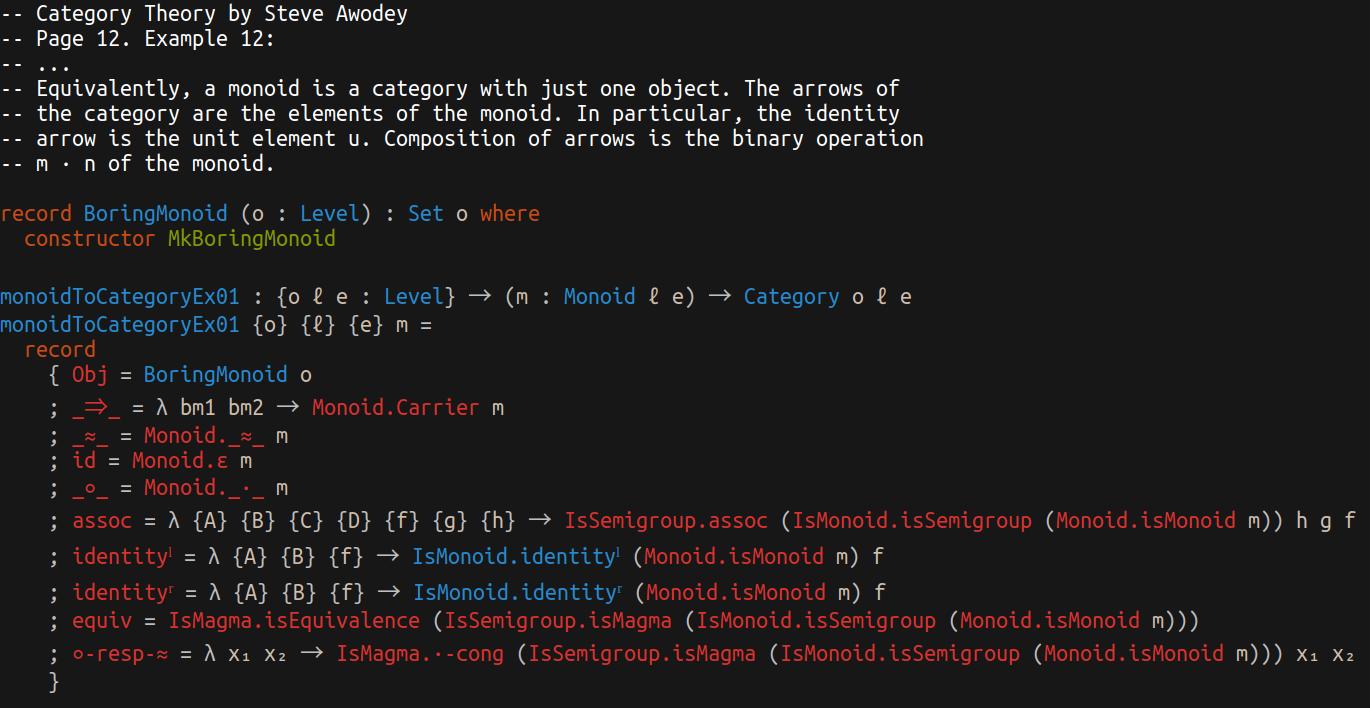
One final note on Agda: I couldn't find TAGS support, but everything you load also integrates with "jump forward/back" in Emacs (C-./C-,), so navigating all the symbol definitions for Monoid and friends was a blast!

p.s.: in cased you've missed the folklore, check out the beautiful StackOverflow explanation of the phrase "A monad is just a monoid in the category of endofunctors, what's the problem?"

Please send your feedback in Issues or PRs in this blog's repo.